The Junior Colloquium is based on the desire to broaden the mathematical horizon of PhD students and postdocs in tower B. It consists of monthly meeting where a PhD student or a postdoc presents a subject, different from his or her own research, that is likely to be of interest for a large audience of mathematicians. The talk aims to be accessible for all. It lasts one hour and is given in English. The event is only for junior researchers (PhD's and postdocs), not senior researchers.
Organizers: - Robynn Corveleyn & Rodrigue Haya Enriquez (2024-?)
- Léo Schelstraete & Benoît Van Vaerenbergh (2022-2024)
The Junior Colloquium usually takes place in the CYCL01, in the Marc de Hemptinne Building.
Upcoming events
Tuesday December 17 (2024), 12h50-13h50, CYCL09A
Arthur Massar — A non-commutative Fourier transform: Trying to find a group duality at the quantum level

The Fourier transform on Rn is one of the most important objects in mathematics, and its construction can be generalized to abelian locally compact groups to give Pontryagin duality. This theory famously fails however for non-commutative groups.
In my research I have come across examples of Fourier transforms which provide a duality between two non-commutative groups after they have been quantized, and I am currently trying to better understand this phenomenon.
We will begin by a short introduction to quantum groups and a review of Pontryagin duality.
We will then try to understand how a similar duality can appear for non-commutative groups at the quantum level.
Past events
Wednesday November 27 (2024), 12h50-13h50, CYCL01
Marthe Ballon (VUB) — Memorisation vs. Reasoning: What the vec happens inside Large Language Models when solving math questions?

The current debate about whether Large Language Models can reason or merely memorise templates is fascinating, as even two of the most prominent experts on the matter, Yann Lecun (Chief AI Meta, Turing Award) and Geoffrey Hinton (Nobel prize, Turing Award) cannot agree. Intuitively, my research starts from the idea that if LLMs can reason (especially math-reasoning), it should be possible to discover - and tune - this in the internal machinery of the model. For example, recent research shows that LLMs construct a scratchpad with necessary parameters/dependencies before answering grade school math questions (Allen-Zhu et al. 2024). This introductory talk will consist of three parts: an overview of the ‘must-knows’ about LLMs as a researcher, a few highlights of relevant previous research, and preliminary results on GPT-4’s ability to solve olympiad-level math questions.
Thursday October 17 (2024), 12h50-13h50, CYCL01
Rodrigue Haya Enriquez — Topology through time: an overview of persistent homology
In different areas of mathematics (geometry, data analysis...), we come across situations where a topological space varies over time. One useful tool to study the evolution of its topology is persistent homology, whose aim is tracking the moments when holes appear and disappear in the space. In this talk, we will define the persistent homology of a simplicial complex and look at ways to visualize it. Depending on time, we will also discuss applications in data analysis by building persistent homologies for point clouds.
Wednesday September 25 (2024), 12h50-13h50, CYCL 09A
Leo Schelstraete — Out of line: a leisure tour on two-dimensional calculus
In mathematics, one is used to one-dimensional calculus: numbers multiply on the left or on the right, functions post- or pre-compose. But certainly one cannot put a function above another one... right? This talk will take you on a leisure tour around the idea of two-dimensional calculus, through examples ranging from topology, algebra, computer science and physics.
Wednesday June 19 (2024), 12h50-13h50, CYCL 01
Leon Winter — Weak partial differential equations and their boundary values

Partial differential equations and boundary value problems are fundamental problems which describe many physical phenomena such as, among many others, heat diffusion through a body or the dynamics of fluids. Depending on the equation, it is not always easy (or even possible) to find analytic solutions, that is, smooth functions which satisfy the partial differential equation. To remedy the situation, the problem is relaxed into a "weak partial differential equation" with a notion of "weak derivative". This allows us to work with a greater class of potential solutions, which are however only defined almost everywhere, up to a set of measure zero. Since the boundary of a smooth domain has measure zero, an important question arises: how, if possible, can we express boundary conditions for weak partial differential equations ?
Wednesday May 15 (2024), 12h50-13h50, CYCL 02
Corentin Vienne — How could we give better talks?

Bryna Kra wrote: "No one likes to sit through a bad talk, but unfortunately everyone does it too frequently. No one sets out to give a bad talk, but probably all of us have done so". In my opinion, it is difficult to disagree with such a statement. To begin with, we will try to understand together why this occurs. Then, we will discuss how to avoid giving bad talks as individuals, but also as a community. The goal of the session will be to share our thoughts on a topic we do not often discuss. Feel free to join and bring some of your fresh ideas.
Monday April 15 (2024), 12h50-13h50, CYCL 01
Simon Mataigne (UCLouvain – ICTEAM) — The enigmatic geometry of the Stiefel manifold: what do high-dimensional surfaces look like?

We give bounds on the geodesic distances on the Stiefel manifold, derived from new geometric insights. These geodesic distances are induced by a previously proposed one-parameter family of Riemannian metrics, which contains the well-known Euclidean and canonical metrics. First, we give the best Lipschitz constants between the distances induced by any two members of the family of metrics. Then, we give a lower and an upper bound on the geodesic distance by the easy-to-compute Frobenius distance. These bounds aim at improving the theoretical guarantees and performance of minimal geodesic computation algorithms by reducing the size of the initial velocity search space. Finally, we also address the question of computing numerically the Riemannian logarithm between any two points, given any member from the family of Riemannian metric. This requires developing efficient iterative schemes solving a nonlinear matrix equation.
Wednesday March 13 (2024), 12h50-13h50, CYCL 01
Julia Ramos González — Sheaves: To glue, or not to glue, or to partly glue, that is the question

Sheaf theory studies and analyses the gluing of local information into global information. Local-to-global situations frequently feature in geometry, but not exclusively, and sheaf theory is nowadays a key tool not only in geometric domains like algebraic topology, analytic geometry or algebraic geometry, but also in category theory and mathematical logic. In this talk we introduce the concept of sheaf and explore its versatility through the analysis of key examples coming from different areas of mathematics.
Tuesday February 20 (2024), 12h50-13h50, CYCL 01
Robynn Corveleyn — A glimpse into the PI world: crossing the Group-Lie bridge

One of the group theorist’s favourite tricks (and certainly one of mine) is to actually study Lie algebras instead of groups. Our question then usually goes something like this: "Can I translate my group problem into a Lie algebra problem? And if I can solve it, can I then also lift my solution back to the group side?" This type of philosophy certainly lies at the basis of the Lie group - Lie algebra correspondence, but that is not the only way to apply this kind of trick. In this talk, we will introduce how to associate a nice Lie algebra to any group we like, and explore how the theory of algebras satisfying a polynomial identity (PI-algebras) helps us in our quest for answers on the group side. In particular we will make some comments on Zelmanov’s solution to the restricted Burnside problem, and our own ongoing work (joint with Geoffrey Janssens).
Monday January 22 (2024), 14h30-15h30, CYCL 01
Damien Galant (UMons) — The nonlinear Schrödinger equation on noncompact graphs : what is a solution
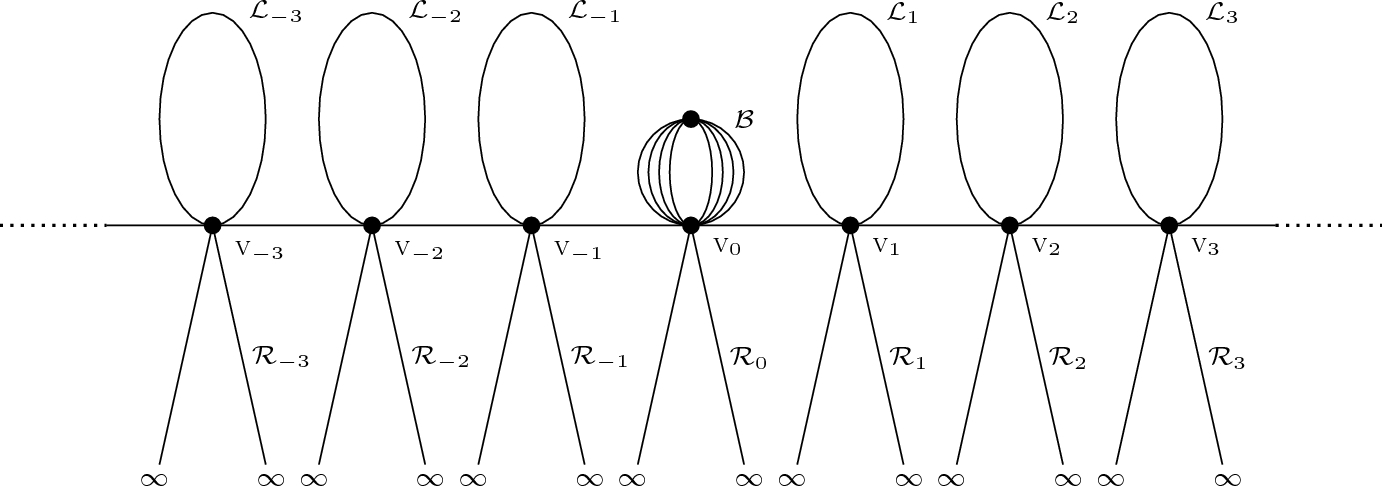
In a first time, we will discover the structures called metric graphs and formulate the (elliptic) nonlinear Schrödinger equation on them. We will then introduce the notion of "ground state" provided by calculus of variations. In a second time, we will see that for noncompact metric graphs, one has to be careful while using the terminology "ground state", and that one should distinguish the notions of "ground state" and of "minimal action solution". During the talk, we will highlight the specific features and advantages offered by the metric graph setting, allowing to use the geometric properties of the domain on which the equation is set. The content of this talk is based on joint work with Colette De Coster (UPHF), Simone Dovetta (Politecnico di Torino), Enrico Serra (Politecnico di Torino) and Christophe Troestler (UMONS). .
Wednesday December 6 (2023), 12h50-13h50, CYCL 01
Maxime Culot — Why abelian groups and groups are so different?

From a group theory point of view, the “only” difference between S3 and Z/6Z is that the (group) product of the first one is non-commutative whereas the second is commutative. This only difference implies that the category of abelian groups Ab and the category of groups Gp are VERY DIFFERENTS from a macroscopic point of view (namely from a categorical point of view). The purpose of my talk is to show some common features and some differences of the two categories. I will also try to convince you why the differences are very "annoying" for my research. Since I would like to give a large audience talk, I will try to avoid as much as possible the category theory language and I will focus on elements proofs. At the end, I would like to conclude with a categorical formalism to sum up all the (common/different) features that we discover in Ab and in Gp.
Friday November 3 (2023), 12h50-13h50, CYCL 01
Louis De Man — The wavefront set or how high pitch sounds give rise to singularities

We can not hear the absolute value function but if we could, it would probably be very unconfortable. Indeed, the singularity at zero implies the presence of high frequency waves in its Fourier decomposition, which means a very high pitch sound. The sound of a smooth function on the other hand, should be way more audible. The goal of this talk is to show how lack of smoothness at finite points of a distribution is triggered by some high frequency directions of its Fourier transform and to define the analytical object encoding this information : the wavefront set. Then we will see how the wavefront set enables to construct algebras of distributions and sometimes to quantized them.
Thursday October 5 (2023), 12h50-13h50, CYCL 02
Daniel Zimmer — Introduction to "Scientific Debate": How To Let Students Formulate and Explore Their Conjectures
One could argue that conjectures and refutations are the heart of the working mathematician’s activity. Yet in high school or elsewhere, mathematical activity is more often than not reduced to sterile exercises and calculations and students hardly have the occasion to develop their own thinking. In this talk/workshop, you will be invited to participate in a mathematical discussion around some problem the way we intend to implement it in classrooms. Such discussion is an opportunity to reflect, argue, doubt, and (hopefully) be convinced ; all activities we would like students to experience in mathematics. The discussion will be followed by some words about ongoing experiments with actual students in Belgian schools.
The slides of the presentation are available here.
Tuesday September 5 (2023), 14h30-15h30, CYCL 01
Alex Loué — The Periodic Table Of Finite Simple Groups

If you have ever set foot into my office, you may have noticed a colorful poster facing me on the wall, looking similar to the periodic table of elements (which you would expect to find in any chemist’s office !). It is suitably called : « The Periodic Table Of Finite Simple Groups ».
Finite simple groups are, in some sense, the atoms of finite groups. Their classification was announced in the early 2000’s, and is most definitely one of the greatest achievements in the history of mathematics. It is also a difficult and extremely intricate subject, so much so that only very few people do have a good picture of the whole thing in mind, even within the group theory community.
My goal will not be to classifiy the finite simple groups, but rather to describe the various families of finite simple groups, how to construct them (which is not always an easy feature) and briefly explain how one could show that they are indeed simple. I will try to give a timeline and there will be many examples along the way which should, hopefully, convey my fascination for the subject (even though I know so little about it).
Friday June 30 (2023), 15h30-17h30, CYCL 01
Fathi Ben Aribi and Jacques Darné — 4-dimensional topology: a holiday tour

Summer is here, and what better way to change scenery than to travel…one dimension higher ? Come join us for a holiday tour in 4-dimensional topology, where several things start to get weird. Spaces that are homeomorphic but not diffeomorphic ?! Sounds pretty exotic ! Also, if you like things to run smoothly on a global scale, wE8 to tell you… it’s not always possible anymore ! Engage in group activities ! Braid some tubes or glue some handlebodies together for surprising results ! Any group is welcome and will find its appropriate 4-manifold to fundamentally fit in. Possibilities are endless, visualization is on the menu, and prerequisites are optional.
Tuesday May 23 (2023), 14h30-15h30, CYCL 01
Nicolas Robert — Random tiling problems and Aztec diamonds
Random tiling problems, or perfect matchings, constitute a class of exactly solvable models studied by both mathematicians and mathematical-physicists since the 20th century. These models can be viewed as a playground where some universal behaviours take place, and they are particularly interesting as much for their links with statistical systems as for their rich mathematical structure. In this presentation, I will introduce and review some basic properties about these models and present standard techniques to obtain their partition functions. I will also speak about tilings of the Aztec diamond and explain how they can be related to random matrix theory.
